Mengeksplorasi Teka-Teki Angka (TTA)

Perhatikan teka-teki angka  berikut ini:

Suatu bilangan terdiri dari empat angka. Angka pertama nilanya sama dengan angka kedua ditambah angka ketiga. Angka pertama juga sama nilainya dengan angka keempat ditambah satu. Begitupula angka kedua ternyata nilainya sama dengan angka ketiga ditambah satu. Bila angka keempat sama dengan dua kali angka ketiga, maka berapa bilangan (empat angka) tersebut?

Teka-teki semacam ini banyak kita temukan dalam buku-buku TTS* atau TTA (Teka-teki Angka) yang sering dijual di kios-kios koran di pinggir jalan. Biasanya para konsumen kedua jenis buku ini adalah mereka-mereka yang punya banyak waktu luang dan suka iseng mengisi waktunya. Ketimbang bengong tak bermanfaat, mending mengisi TTS atau TTA. Begitu barangkali alasannya. Betul ga?
Dulu, ketika melihat banyak orang yang begitu asyik mengerjakan TTS ataupun TTA, saya jadi tergoda. Ya, saya tergoda untuk mengerjakannya pula. Kemudian dapat ditebak, saya pun membeli kedua jenis buku ini. Satu buku TTS dan satu buku lagi TTA.

TTS sudah biasa! Ya, saya biasa mengalami kesulitan untuk mengisi semua kotak-kotak kosong yang tersedia. Mungkin karena tak terbiasa ataupun karena pengetahuan saya yang minim. Makanya sukar bagi saya bisa mengisi keseluruhan kotak kosong dalam sebuah TTS.

Kemudian buku TTA saya buka. Saya lihat-lihat. Satu jenis teka-teki yang ada dalam buku TTA yang saya beli yakni seperti teka-teki angka pada contoh di atas. Ketika membaca teka-teki semacam contoh tersebut, saya melihat sebetulnya teka-teki semacam itu menggunakan konsep matematika sederhana yang pernah saya kita pelajari sewaktu di SMP dan SMA, yaitu tentang sistem persamaan linear. Tetapi, setelah dipikir-pikir, untuk menyelesaikan teka-teki angka semacam itu, kita tak harus tahu sistem persamaan linear. Cukup dengan cara coba-coba alias trial and error bila kita beruntung, maka kita akan dapat memecahkan teka-teki tersebut.
Sebagai contoh, mari kita selesaikan teka-teki di atas dengan cara coba-coba seperti berikut ini.

Suatu bilangan terdiri dari empat angka. (Kita ingat-ingat, berarti bilangannya ada empat digit/angka. )
Angka pertama nilanya sama dengan angka kedua ditambah angka ketiga. (Kita pilih angka pertama misalkan . Kita ingat-ingat juga angka ini merupakan jumlah dari angka kedua dan ketiga, ini berarti angka kedua atau ketiga nilanya lebih kecil atau sama dari angka pertama.)
Angka pertama sama nilainya dengan angka keempat ditambah satu. (Karena tadi kita sudah pilih angka pertama adalah , maka dari keterangan ini dapat kita tentukan angka keempat yakni , sebab ).
Begitupula angka kedua ternyata nilainya sama dengan angka ketiga ditambah satu. (Karena angka kedua dan ketiga lebih kecil dari angka pertama, kita pilih angka kedua itu . Sehingga, angka ketiga berarti , sebab .)
Bila angka keempat sama dengan dua kali angka ketiga, (Kita sudah tahu angka keempat yaitu dan ini cocok dengan pilihan kita tentang angka ketiga, yakni .
maka berapa bilangan (empat angka) tersebut?
Maka jawabnya, bilangan empat angka itu adalah .

Dengan cara coba-coba, ternyata kita dapat memecahkan teka-teki angka tersebut. Jawabannya yaitu . Tetapi sebentar, jangan gembira dulu, apakah ini satu-satunya jawaban?
Ternyata tidak! Setelah dipikir-pikir, ternyata bilangan juga memenuhi persyaratan teka-teki tersebut. (Silakan periksa! ). Ternyata juga bilangan memenuhi persyaratan teka-teki angka tersebut.
Lho, kok bisa banyak jawaban begini ya?

Sebetulnya banyak jawaban tidaklah bermasalah. Malah teka-teki tersebut tergolong sangat bagus. Satu permasalahan dengan banyak alternative jawaban. Istilah kerennya, teka-teki yang bersifat open-ended.
Pertanyaannya, ada berapa banyak alternative jawaban dari teka-teki angka tersebut?
Nah, di sinilah peran konsep matematika diperlukan! Dengan menggunakan konsep matematika, kemungkinan besar kita akan tahu alasan kenapa banyak jawaban. Dengan itu pula mungkin sekali kita tahu semua alternative jawabannya. Karena itu mari kita selesaikan teka-teki angka tersebut dengan konsep sistem persamaan linear seperti berikut ini.

Misalkan bilangan itu adalah .

Maka sesuai keterangan pada teka-teki di atas, diperoleh sistem persamaan linear berikut ini.

dan .

Dengan mudah, bila kita pilih 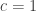, maka kita akan peroleh , , dan . Sehingga bilangan sebagai satu alternative jawaban teka-teki angka di atas adalah .

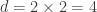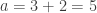Begitu pula bila kita pilih , maka akan kita dapatkan , , dan . Sehingga jawaban lain dari teka-teki di atas adalah .

Dengan memilih nilai yang lain, maka kita akan dapatkan jawaban lain dari teka-teki angka tersebut. Silakan cari sendiri yaaa….

Nah, asyik bukan?

Sekarang, sebagai bahan latihan bagi kita Anda semua, silakan buat teka-teki angka semacam di atas, kemudian silakan jawab sendiri, silakan eksplorasi sendiri teka-teki angka buatan Anda! Selamat mencoba! I hope you enjoy doing mathematics.  And, in a similar way, I hope you can not stop loving me mathematics.

========================================================

Segitu dulu ya perjumpaan kita kali ini. Mudah-mudahan artikel ini bermanfaat bagi kita semua. Amin. Sampai jumpa di artikel mendatang.

Posted in matematika